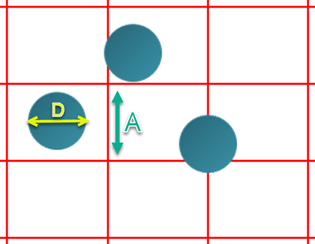
Problem: If a coin with a diameter of D is tossed and lands on a square tile of side A, what is the probability that the coin will land on tile’s edge or fall completely within the tile?

Analytical solution:

The probability of a coin to land on tile’s edge is the complementary probability of the coin to fall completely within the tile. Let’s denote with p, the probability of the coin of falling completely within the tile, when the theoretical probability can be given by:

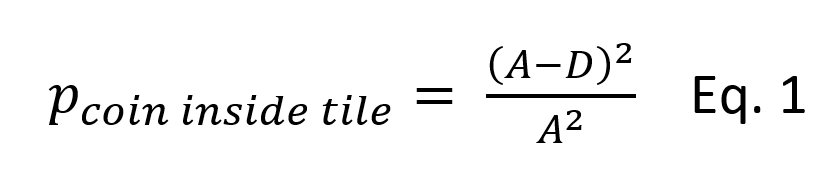
For a coin with diameter of D, the centre of the coin must be D/2 away from any edge of the tile. Therefore, the coin must be within a square of side A−D. If the centre of the coin is distributed uniformly within the tile, the chance of it being inside the smaller square—and thus completely within the tile is given by equation (1).

Numerical solutions:

Here, we will develop an application to simulate the toss of a coin over the square tile. To solve this, we need to generate random positions of the centre of the coin within the square tile, check if the coin is landed on any tile’s edge. Finally, we need to repeat the above process for M times, and count the times (N_hits), the coin overlaps any of the edges. The probability in question is given by: 

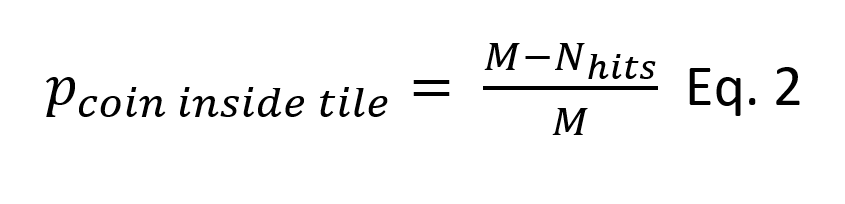
The application:

First we are going to develop a library that delivers the required functionality for our simulations. The initial projects in the MS Visual Studio are:

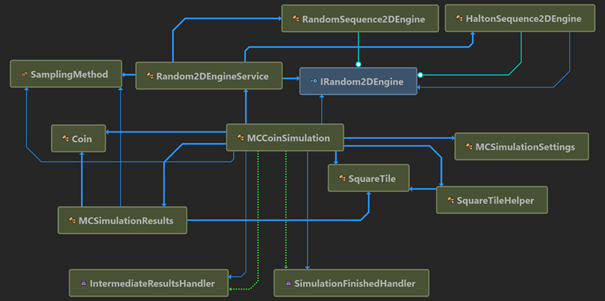
The basic elements of the library (MCCoinLib) are Coin, SquareTile, RandomEngine, MCSimulationSettings, MCSimulationResults and MCCoinSimulation objects.

In the following figure the inter-dependency of the objects within MCCoinLib is shown:

Running the code:

static void Main(string[] args)
{
	var settings = MCSimulationSettings.Create(numberTrials: 100000, 
                                 reportEveryIteration: 100);
	var randomEngineService = new Random2DEngineService();

	MCCoinSimulation simulation = new MCCoinSimulation(settings, 
                                  randomEngineService);
           
    simulation.Finished += results => {
      Console.WriteLine($"MC simulation finished.\n{results}");
    };

    simulation.Run(Coin.CreateWithDiameter(1.0), 
     				SquareTile.Create(2.0), 
                    SamplingMethod.Halton);
	Console.ReadKey();
}

The console output is:

MC simulation finished.
 Input data:
 (1) coin with diameter = 1
 (2) square tile of size = 2x2
 (3) sampling method: Halton
 The coin has probability of 0.750001 to land on the square edges.

We can run the simulation using a uniform random engine for sampling point generation, as follows:

simulation.Run(Coin.CreateWithDiameter(1.0),
                SquareTile.Create(2.0),
                SamplingMethod.RandomUniform);

The results are:

MC simulation finished.
 Input data:
 (1) coin with diameter = 1
 (2) square tile of size = 2x2
 (3) sampling method: RandomUniform
 The coin has probability of 0.750443 to land on the square edges.

The full code is available on https://github.com/isachpaz/MonteCarloApp

Further reading/videos: